Archimedes

1.1. Kerjaya

Versi standard kehidupan Archimedes ditulis lama selepas kematiannya oleh ahli sejarah Yunani dan Rom. Rujukan terawal kepada Archimedes berlaku dalam Sejarah oleh Polybius (kira-kira 200-118 SM), yang ditulis kira-kira 70 tahun selepas kematiannya. Ia sedikit memberi penerangan tentang Archimedes sebagai seorang individu, dan lebih menumpukan kepada mesin perang yang dikatakan telah dibina untuk mempertahankan kota daripada orang Rom. Polybius menyatakan bagaimana, semasa Perang Punic Kedua, Syracuse menukar kesetiaan daripada Republik Rom kepada Carthage, menyebabkan kempen ketenteraan di bawah pimpinan Marcus Claudius Marcellus dan Appius Claudius Pulcher, yang mengepung kota itu dari 213 hingga 212 SM. Beliau menyatakan bahawa orang Rom memandang rendah pertahanan Syracuse, dan menyebut beberapa mesin yang direka oleh Archimedes, termasuk katapel yang diperbaiki, mesin seperti kren yang boleh diayunkan dalam lengkok, dan pelontar batu yang lain. Walaupun orang Rom akhirnya menawan kota itu, mereka mengalami kerugian besar akibat kepintaran Archimedes.

Cicero (106-43 SM) menyebut Archimedes dalam beberapa karyanya. Semasa berkhidmat sebagai kuaestor di Sicily, Cicero menemui apa yang dianggap sebagai makam Archimedes berhampiran pintu Agrigentine di Syracuse, dalam keadaan terbiar dan ditumbuhi semak. Cicero membersihkan makam itu dan dapat melihat ukiran serta membaca beberapa ayat yang telah ditambah sebagai prasasti. Makam itu mempunyai ukiran yang menggambarkan bukti matematik kegemaran Archimedes, bahawa isi padu dan luas permukaan sfera adalah dua pertiga daripada silinder yang melingkunginya termasuk tapaknya. Beliau juga menyebut bahawa Marcellus membawa ke Rom dua planetarium yang dibina oleh Archimedes. Ahli sejarah Rom Livy (59 SM-17 M) menceritakan semula kisah Polybius tentang penawanan Syracuse dan peranan Archimedes di dalamnya.

1.2. Kematian

Plutarch (45-119 M) memberikan sekurang-kurangnya dua versi tentang bagaimana Archimedes meninggal dunia selepas Syracuse ditawan. Menurut versi yang paling popular, Archimedes sedang merenung rajah matematik apabila kota itu ditawan. Seorang askar Rom mengarahkannya untuk datang dan berjumpa Marcellus, tetapi beliau menolak, mengatakan bahawa beliau perlu menyelesaikan masalah itu. Ini membuat askar itu marah, lalu membunuh Archimedes dengan pedangnya. Kisah lain pula menceritakan Archimedes membawa alat matematik sebelum dibunuh kerana seorang askar menyangka ia adalah barang berharga. Marcellus dilaporkan marah dengan kematian Archimedes, kerana beliau menganggapnya sebagai aset saintifik yang berharga (beliau memanggil Archimedes "Briareus geometri") dan telah mengarahkan agar beliau tidak dicederakan.

Kata-kata terakhir yang dikaitkan dengan Archimedes ialah "Jangan ganggu bulatan saya" (Noli turbare circulos meos^{Bahasa Latin}; μὴ μου τοὺς κύκλους τάραττε^{Bahasa Yunani, Moden}), merujuk kepada lukisan matematik yang kononnya sedang dipelajari oleh beliau apabila diganggu oleh askar Rom. Tiada bukti yang boleh dipercayai bahawa Archimedes mengucapkan kata-kata ini dan ia tidak muncul dalam catatan Plutarch. Petikan yang serupa ditemui dalam karya Valerius Maximus (fl. 30 M), yang menulis dalam Perbuatan dan Kata-kata yang Mengingatkan, "... tetapi melindungi debu dengan tangannya, berkata 'Saya mohon, jangan ganggu ini'".

2.1. Kaedah Kehabisan dan Infinitesimal

Archimedes dapat menggunakan indivisibel (pelopor kepada infinitesimal) dengan cara yang serupa dengan kalkulus kamiran moden. Melalui bukti dengan kontradiksi (reductio ad absurdum), beliau dapat memberikan jawapan kepada masalah pada tahap ketepatan arbitrari, sambil menyatakan had di mana jawapan itu berada. Teknik ini dikenali sebagai kaedah kehabisan, dan beliau menggunakannya untuk menganggarkan luas bentuk dan nilai Pi (π).

2.2. Anggaran Pi

Dalam Pengukuran Bulatan, beliau melakukannya dengan melukis heksagon biasa yang lebih besar di luar bulatan kemudian heksagon biasa yang lebih kecil di dalam bulatan, dan secara progresif menggandakan bilangan sisi setiap poligon biasa, mengira panjang sisi setiap poligon pada setiap langkah. Apabila bilangan sisi meningkat, ia menjadi anggaran yang lebih tepat bagi bulatan. Selepas empat langkah sedemikian, apabila poligon mempunyai 96 sisi setiap satu, beliau dapat menentukan bahawa nilai π terletak antara 3 1/7 (kira-kira 3.1429) dan 3 10/71 (kira-kira 3.1408), konsisten dengan nilai sebenar kira-kira 3.1416. Beliau juga membuktikan bahawa luas bulatan adalah sama dengan π didarab dengan kuasa dua jejari bulatan (πr²).

2.3. Geometri

Archimedes membuktikan bahawa luas bulatan adalah sama dengan π didarab dengan kuasa dua jejari bulatan (πr²). Dalam Mengenai Sfera dan Silinder, beliau memperoleh hasil yang paling dibanggakan, iaitu hubungan antara sfera dan silinder yang melingkungi dengan ketinggian dan diameter yang sama. Isi padu sfera ialah 4/3πr³, dan untuk silinder ialah 2πr³. Luas permukaan sfera ialah 4πr², dan untuk silinder ialah 6πr² (termasuk dua tapaknya), di mana r ialah jejari sfera dan silinder.

Dalam Kuadratur Parabola, Archimedes membuktikan bahawa luas yang dikelilingi oleh parabola dan garis lurus adalah 4/3 kali luas segitiga terpahat yang sepadan seperti yang ditunjukkan dalam rajah di sebelah kanan. Beliau menyatakan penyelesaian masalah itu sebagai siri geometri tak terhingga dengan nisbah sepunya 1/4.
Jika sebutan pertama dalam siri ini ialah luas segitiga, maka yang kedua ialah hasil tambah luas dua segitiga yang tapaknya ialah dua garis sekan yang lebih kecil, dan bucu ketiga ialah tempat garis yang selari dengan paksi parabola dan yang melalui titik tengah tapak bersilang dengan parabola, dan seterusnya. Bukti ini menggunakan variasi siri 1/4 + 1/16 + 1/64 + 1/256 + · · · yang berjumlah 1/3.

Dalam Mengenai Konoid dan Sferoid, Archimedes mengira luas dan isi padu keratan kon, sfera, dan paraboloid.

2.4. Sifat Archimedes

Dalam Mengenai Sfera dan Silinder, Archimedes mengandaikan bahawa sebarang magnitud apabila ditambah kepada dirinya sendiri beberapa kali akan melebihi sebarang magnitud yang diberikan. Hari ini ini dikenali sebagai sifat Archimedes bagi nombor nyata.

Archimedes memberikan nilai punca kuasa dua bagi 3 sebagai terletak antara 265/153 (kira-kira 1.7320261) dan 1351/780 (kira-kira 1.7320512) dalam Pengukuran Bulatan. Nilai sebenar adalah kira-kira 1.7320508, menjadikan ini anggaran yang sangat tepat. Beliau memperkenalkan hasil ini tanpa menawarkan sebarang penjelasan tentang bagaimana beliau memperolehinya. Aspek karya Archimedes ini menyebabkan John Wallis menyatakan bahawa beliau: "seolah-olah sengaja menyembunyikan jejak penyiasatannya seolah-olah beliau cemburu akan rahsia kaedah penyelidikannya kepada generasi akan datang sementara beliau ingin memaksa mereka bersetuju dengan hasilnya." Ada kemungkinan beliau menggunakan prosedur lelaran untuk mengira nilai-nilai ini.

2.5. Penghitung Pasir

Dalam Penghitung Pasir, Archimedes bertujuan untuk mengira bilangan butir pasir yang lebih besar daripada yang diperlukan untuk mengisi alam semesta. Dengan berbuat demikian, beliau mencabar tanggapan bahawa bilangan butir pasir terlalu besar untuk dikira. Beliau menulis:
"Ada beberapa, Raja Gelo, yang berpendapat bahawa bilangan pasir adalah tak terhingga; dan yang saya maksudkan dengan pasir bukan sahaja yang wujud di sekitar Syracuse dan Sicily yang lain tetapi juga yang terdapat di setiap wilayah sama ada berpenghuni atau tidak berpenghuni."
Untuk menyelesaikan masalah itu, Archimedes mencipta sistem pengiraan berdasarkan myriad. Perkataan itu sendiri berasal dari bahasa Yunani μυριάς^{Bahasa Yunani, Purba}, untuk nombor 10,000. Beliau mencadangkan sistem nombor menggunakan kuasa myriad daripada myriad (100 juta, iaitu 10,000 x 10,000) dan menyimpulkan bahawa bilangan butir pasir yang diperlukan untuk mengisi alam semesta ialah 8 vigintillion, atau 8 x 10⁶³.

2.6. Karya Matematik Utama

• Pengukuran Bulatan: Sebuah karya pendek yang mengandungi tiga usul. Ia ditulis dalam bentuk surat-menyurat dengan Dositheus dari Pelusium. Archimedes memberikan anggaran nilai pi (π) antara 3 1/7 dan 3 10/71.
• Kuadratur Parabola: Dalam karya ini yang mengandungi 24 usul yang ditujukan kepada Dositheus, Archimedes membuktikan bahawa luas yang dikelilingi oleh parabola dan garis lurus adalah 4/3 kali luas segitiga dengan tapak dan ketinggian yang sama.
• Mengenai Sfera dan Silinder: Dalam risalah dua jilid ini yang ditujukan kepada Dositheus, Archimedes memperoleh hasil yang paling dibanggakan, iaitu hubungan antara sfera dan silinder yang melingkungi dengan ketinggian dan diameter yang sama.
• Mengenai Spiral: Karya ini yang mengandungi 28 usul juga ditujukan kepada Dositheus. Risalah ini mendefinisikan apa yang kini dipanggil spiral Archimedes.
• Mengenai Konoid dan Sferoid: Ini adalah karya dalam 32 usul yang ditujukan kepada Dositheus. Dalam risalah ini Archimedes mengira luas dan isi padu keratan kon, sfera, dan paraboloid.
• Mengenai Keseimbangan Satah: Terdapat dua buku untuk Mengenai Keseimbangan Satah: yang pertama mengandungi tujuh aksiom dan lima belas usul, manakala buku kedua mengandungi sepuluh usul. Dalam buku pertama, Archimedes membuktikan hukum tuas.
• Ostomachion: Juga dikenali sebagai Lokulus Archimedes atau Kotak Archimedes, ini adalah teka-teki pembahagian yang serupa dengan Tangram, dan risalah yang menerangkannya ditemui dalam bentuk yang lebih lengkap dalam Palimpsest Archimedes.
• Masalah Lembu Archimedes: Karya ini ditemui oleh Gotthold Ephraim Lessing dalam manuskrip Yunani yang terdiri daripada puisi 44 baris. Ia ditujukan kepada Eratosthenes dan ahli matematik di Alexandria. Archimedes mencabar mereka untuk mengira bilangan lembu dalam Kawanan Matahari dengan menyelesaikan beberapa persamaan Diophantine serentak.
• Kaedah Teorem Mekanikal: Risalah ini dianggap hilang sehingga penemuan Palimpsest Archimedes pada tahun 1906. Dalam karya ini Archimedes menggunakan indivisibel, dan menunjukkan bagaimana memecahkan bentuk menjadi bilangan bahagian yang tak terhingga kecil boleh digunakan untuk menentukan luas atau isi padunya.

3.1. Prinsip Keterapungan (Kisah Eureka)

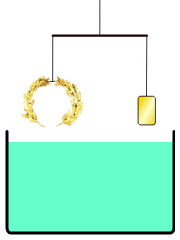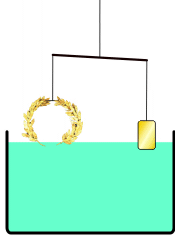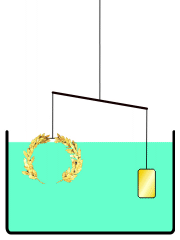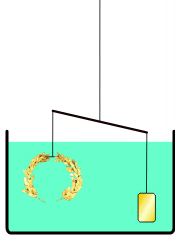
Anekdot yang paling terkenal tentang Archimedes menceritakan bagaimana beliau mencipta kaedah untuk menentukan isi padu objek dengan bentuk yang tidak teratur. Menurut Vitruvius, sebuah mahkota untuk kuil telah dibuat untuk Raja Hiero II dari Syracuse, yang membekalkan emas tulen untuk digunakan. Mahkota itu kemungkinan besar dibuat dalam bentuk karangan bunga votif. Archimedes diminta untuk menentukan sama ada sebahagian perak telah digantikan oleh tukang emas tanpa merosakkan mahkota, jadi beliau tidak dapat meleburkannya menjadi badan berbentuk biasa untuk mengira ketumpatannya.

Dalam akaun ini, Archimedes menyedari semasa mandi bahawa paras air di dalam tab mandi naik apabila beliau masuk, dan menyedari bahawa kesan ini boleh digunakan untuk menentukan isi padu mahkota emas. Archimedes begitu teruja dengan penemuan ini sehingga beliau keluar ke jalanan tanpa berpakaian, terlupa untuk berpakaian, sambil menjerit "Eureka!" (εὕρηκα^{Bahasa Yunani, Moden}, heúrēka!, "Saya telah menemuinya!"). Untuk tujuan praktikal air adalah tidak boleh dimampatkan, jadi mahkota yang tenggelam akan menggantikan jumlah air yang sama dengan isi padunya sendiri. Dengan membahagikan jisim mahkota dengan isi padu air yang digantikan, ketumpatannya boleh diperoleh; jika logam yang lebih murah dan kurang tumpat telah ditambah, ketumpatan akan lebih rendah daripada emas. Archimedes mendapati bahawa inilah yang berlaku, membuktikan bahawa perak telah dicampurkan.

Kisah mahkota emas tidak muncul di mana-mana dalam karya Archimedes yang diketahui. Kepraktisan kaedah yang diterangkan telah dipersoalkan kerana ketepatan melampau yang diperlukan untuk mengukur anjakan air. Archimedes mungkin sebaliknya mencari penyelesaian yang mengaplikasikan prinsip hidrostatik yang dikenali sebagai Prinsip Archimedes, yang terdapat dalam risalahnya Mengenai Jasad Terapung: jasad yang tenggelam dalam cecair mengalami daya apung yang sama dengan berat cecair yang digantikannya. Menggunakan prinsip ini, adalah mungkin untuk membandingkan ketumpatan mahkota dengan emas tulen dengan mengimbangkannya pada skala dengan sampel rujukan emas tulen dengan berat yang sama, kemudian merendam alat itu dalam air. Perbezaan ketumpatan antara kedua-dua sampel akan menyebabkan skala condong dengan sewajarnya. Galileo Galilei, yang mencipta imbangan hidrostatik pada tahun 1586 yang diilhamkan oleh karya Archimedes, menganggapnya "kemungkinan kaedah ini adalah sama dengan yang diikuti oleh Archimedes, kerana, selain sangat tepat, ia berdasarkan demonstrasi yang ditemui oleh Archimedes sendiri."

3.2. Hukum Tuas

Walaupun Archimedes tidak mencipta tuas, beliau memberikan bukti matematik prinsip yang terlibat dalam karyanya Mengenai Keseimbangan Satah. Penerangan awal prinsip tuas ditemui dalam karya Euclid dan dalam Masalah Mekanikal, milik sekolah Peripatetik pengikut Aristotle, yang pengarangnya telah dikaitkan oleh sesetengah pihak kepada Archytas.

Terdapat beberapa laporan, sering bercanggah, mengenai pencapaian Archimedes menggunakan tuas untuk mengangkat objek yang sangat berat. Plutarch menerangkan bagaimana Archimedes mereka bentuk sistem takal takal majmuk, membolehkan pelayar menggunakan prinsip daya ungkit untuk mengangkat objek yang sebaliknya terlalu berat untuk digerakkan. Menurut Pappus dari Alexandria, karya Archimedes mengenai tuas dan pemahamannya tentang kelebihan mekanikal menyebabkan beliau berkata: "Berikan saya tempat untuk berdiri, dan saya akan menggerakkan Bumi" (δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω^{Bahasa Yunani, Moden}). Olympiodorus kemudiannya mengaitkan kebanggaan yang sama kepada ciptaan Archimedes iaitu baroulkos, sejenis winch, dan bukannya tuas.

3.3. Statik dan Hidrostatik

Dalam Mengenai Jasad Terapung, Archimedes menjelaskan hukum keseimbangan cecair dan membuktikan bahawa air akan mengambil bentuk sfera di sekeliling pusat graviti. Ini mungkin merupakan cubaan untuk menjelaskan teori ahli astronomi Yunani kontemporari seperti Eratosthenes bahawa Bumi adalah bulat. Cecair yang diterangkan oleh Archimedes tidak graviti sendiri kerana beliau mengandaikan kewujudan titik di mana semua benda jatuh untuk mendapatkan bentuk sfera. Prinsip Archimedes tentang daya apung diberikan dalam karya ini, dinyatakan seperti berikut:
"Mana-mana jasad yang tenggelam sepenuhnya atau sebahagiannya dalam cecair mengalami daya tujah ke atas yang sama dengan, tetapi bertentangan arah dengan, berat cecair yang digantikan."
Dalam bahagian kedua, beliau mengira kedudukan keseimbangan keratan paraboloid. Ini mungkin merupakan idealisasi bentuk badan kapal. Beberapa keratannya terapung dengan tapak di bawah air dan puncak di atas air, serupa dengan cara aisberg terapung.

3.4. Ciptaan

3.4.1. Skru Archimedes

Sebahagian besar kerja Archimedes dalam kejuruteraan mungkin timbul daripada memenuhi keperluan kota asalnya Syracuse. Athenaeus dari Naucratis memetik seorang Moschion dalam penerangan tentang bagaimana Raja Hiero II menugaskan reka bentuk kapal besar, Syracusia, yang boleh digunakan untuk perjalanan mewah, membawa bekalan, dan sebagai pameran kuasa tentera laut. Syracusia dikatakan sebagai kapal terbesar yang dibina pada zaman purba klasik dan, menurut catatan Moschion, ia dilancarkan oleh Archimedes. Kapal itu kononnya mampu membawa 600 orang dan termasuk hiasan taman, gimnasium, dan kuil yang didedikasikan kepada dewi Aphrodite antara kemudahannya. Catatan itu juga menyebut bahawa, untuk membuang sebarang air yang mungkin bocor melalui badan kapal, sebuah peranti dengan bilah berbentuk skru berputar di dalam silinder telah direka oleh Archimedes.

Skru Archimedes diputar dengan tangan, dan juga boleh digunakan untuk memindahkan air dari badan air yang rendah ke saluran pengairan. Skru itu masih digunakan hari ini untuk mengepam cecair dan pepejal berbutir seperti arang batu dan bijirin. Diterangkan oleh Vitruvius, peranti Archimedes mungkin merupakan penambahbaikan pada pam skru yang digunakan untuk mengairi Taman Gantung Babylon. Kapal wap pertama di dunia yang menggunakan kipas skru ialah SS Archimedes, yang dilancarkan pada tahun 1839 dan dinamakan sempena Archimedes dan karyanya mengenai skru.

4.1. Karya yang Bertahan

Karya-karya Archimedes yang masih wujud termasuk:

• Mengenai Keseimbangan Satah
• Mengenai Spiral
• Pengukuran Bulatan
• Mengenai Sfera dan Silinder
• Mengenai Jasad Terapung
• Kaedah Teorem Mekanikal
• Ostomachion
• Masalah Lembu Archimedes
• Penghitung Pasir
• Mengenai Konoid dan Sferoid

4.2. Karya yang Hilang

Beberapa karya Archimedes hanya diketahui melalui rujukan oleh penulis-penulis kuno lain, termasuk:

• Mengenai Pembuatan Sfera
• Karya mengenai polihedron
• Catoptrica (mengenai optik)
• Prinsip (menjelaskan sistem nombor yang digunakan dalam Penghitung Pasir)
• Mengenai Imbangan atau Mengenai Tuas
• Mengenai Pusat Graviti
• Mengenai Kalendar

4.3. Palimpsest Archimedes

Dokumen terpenting yang mengandungi karya Archimedes ialah Palimpsest Archimedes. Pada tahun 1906, profesor Denmark Johan Ludvig Heiberg melawat Constantinople untuk memeriksa kertas kulit kulit kambing setebal 174 halaman yang mengandungi doa-doa, yang ditulis pada abad ke-13, selepas membaca transkripsi pendek yang diterbitkan tujuh tahun sebelumnya oleh Papadopoulos-Kerameus. Beliau mengesahkan bahawa ia memang sebuah palimpsest, sebuah dokumen dengan teks yang telah ditulis di atas karya lama yang dipadamkan. Palimpsest dicipta dengan mengikis dakwat dari karya sedia ada dan menggunakannya semula, amalan biasa pada Zaman Pertengahan, kerana vellum mahal. Karya-karya lama dalam palimpsest itu dikenal pasti oleh sarjana sebagai salinan abad ke-10 bagi risalah-risalah Archimedes yang sebelum ini hilang. Kertas kulit itu menghabiskan ratusan tahun di perpustakaan biara di Constantinople sebelum dijual kepada pengumpul persendirian pada tahun 1920-an. Pada 29 Oktober 1998, ia dijual di lelongan kepada pembeli tanpa nama dengan jumlah 2.20 M USD.

Palimpsest itu mengandungi tujuh risalah, termasuk satu-satunya salinan Mengenai Jasad Terapung yang masih ada dalam bahasa Yunani asal. Ia adalah satu-satunya sumber yang diketahui bagi Kaedah Teorem Mekanikal, yang dirujuk oleh Suda dan dianggap telah hilang selama-lamanya. Stomachion juga ditemui dalam palimpsest, dengan analisis teka-teki yang lebih lengkap daripada yang ditemui dalam teks-teks sebelumnya. Palimpsest itu disimpan di Muzium Seni Walters di Baltimore, Maryland, di mana ia telah menjalani pelbagai ujian moden termasuk penggunaan ultraviolet dan sinar-X untuk membaca teks yang ditulis semula.

Risalah-risalah dalam Palimpsest Archimedes termasuk:

• Mengenai Keseimbangan Satah
• Mengenai Spiral
• Pengukuran Bulatan
• Mengenai Sfera dan Silinder
• Mengenai Jasad Terapung
• Kaedah Teorem Mekanikal
• Stomachion
• Ucapan oleh ahli politik abad ke-4 SM Hypereides
• Ulasan mengenai Kategori Aristotle
• Karya-karya lain

5.1. Impak terhadap Matematik dan Fizik

Ahli sejarah sains dan matematik hampir secara sejagat bersetuju bahawa Archimedes adalah ahli matematik terbaik dari zaman purba. Eric Temple Bell, sebagai contoh, menulis:
"Mana-mana senarai tiga ahli matematik "terhebat" sepanjang sejarah akan memasukkan nama Archimedes. Dua lagi yang biasanya dikaitkan dengannya ialah Newton dan Gauss. Sesetengah pihak, mengambil kira kekayaan-atau kemiskinan-matematik dan sains fizikal dalam zaman masing-masing di mana gergasi-gergasi ini hidup, dan menganggarkan pencapaian mereka berdasarkan latar belakang zaman mereka, akan meletakkan Archimedes di tempat pertama."
Begitu juga, Alfred North Whitehead dan George F. Simmons berkata tentang Archimedes:
"... pada tahun 1500 Eropah tahu kurang daripada Archimedes yang meninggal dunia pada tahun 212 SM ..."
"Jika kita mempertimbangkan apa yang semua manusia lain capai dalam matematik dan fizik, di setiap benua dan dalam setiap tamadun, dari permulaan masa hingga abad ketujuh belas di Eropah Barat, pencapaian Archimedes melebihi semuanya. Beliau adalah tamadun yang hebat dengan sendirinya."
Reviel Netz, Profesor Suppes dalam Matematik dan Astronomi Yunani di Universiti Stanford dan pakar dalam Archimedes menyatakan:
"Oleh itu, kerana Archimedes lebih daripada sesiapa pun yang membawa kepada pembentukan kalkulus dan kerana beliau adalah perintis aplikasi matematik kepada dunia fizikal, ternyata sains Barat hanyalah satu siri nota kaki kepada Archimedes. Oleh itu, ternyata Archimedes adalah saintis terpenting yang pernah hidup."
Leonardo da Vinci berulang kali menyatakan kekaguman terhadap Archimedes, dan mengaitkan ciptaannya Architonnerre kepada Archimedes. Galileo Galilei memanggilnya "luar biasa" dan "tuan saya", manakala Christiaan Huygens berkata, "Saya fikir Archimedes tidak dapat dibandingkan dengan sesiapa pun", secara sedar menirunya dalam karya awalnya. Gottfried Wilhelm Leibniz berkata, "Sesiapa yang memahami Archimedes dan Apollonius akan kurang mengagumi pencapaian tokoh-tokoh terkemuka zaman kemudian". Wira Gauss ialah Archimedes dan Newton, dan Moritz Cantor, yang belajar di bawah Gauss di Universiti Göttingen, melaporkan bahawa beliau pernah berkata dalam perbualan bahawa "hanya ada tiga ahli matematik yang membuat zaman: Archimedes, Newton, dan Eisenstein".

Pencipta Nikola Tesla memuji beliau, dengan berkata:
"Archimedes adalah idola saya. Saya mengagumi karya-karya seniman, tetapi pada pandangan saya, ia hanyalah bayangan dan rupa. Pencipta, saya fikir, memberikan kepada dunia ciptaan yang nyata, yang hidup dan berfungsi."

5.2. Penghormatan dan Peringatan

Numismatis dan ahli arkeologi Itali Filippo Paruta (1552-1629) dan Leonardo Agostini (1593-1676) melaporkan tentang syiling gangsa di Sicily dengan potret Archimedes di bahagian depan dan silinder serta sfera dengan monogram ARMD dalam bahasa Latin di bahagian belakang. Walaupun syiling itu kini hilang dan tarikhnya tidak diketahui dengan tepat, Ivo Schneider menggambarkan bahagian belakang sebagai "sfera yang terletak di atas tapak - mungkin imej kasar salah satu planetarium yang dicipta oleh Archimedes," dan mencadangkan ia mungkin telah ditempa di Rom untuk Marcellus yang "menurut laporan kuno, membawa dua sfera Archimedes bersamanya ke Rom".

Terdapat kawah hentaman di Bulan yang dinamakan Archimedes (29.7° N, 4.0° W) sebagai penghormatan kepadanya, serta banjaran gunung bulan, Montes Archimedes (25.3° N, 4.6° W).

Pingat Fields untuk pencapaian cemerlang dalam matematik membawa potret Archimedes, bersama dengan ukiran yang menggambarkan bukti beliau mengenai sfera dan silinder. Prasasti di sekeliling kepala Archimedes adalah petikan yang dikaitkan dengan penyair abad ke-1 Masihi Manilius, yang berbunyi dalam bahasa Latin: Transire suum pectus mundoque potiri ("Melampaui diri sendiri dan menguasai dunia").

Archimedes telah muncul di setem pos yang dikeluarkan oleh Jerman Timur (1973), Greece (1983), Itali (1983), Nicaragua (1971), San Marino (1982), dan Sepanyol (1963).

Seruan Eureka! yang dikaitkan dengan Archimedes adalah moto negeri California. Dalam hal ini, perkataan itu merujuk kepada penemuan emas berhampiran Sutter's Mill pada tahun 1848 yang mencetuskan demam emas California.